Normatização vs. Realidade: o que considerar certo ou errado na hora H?
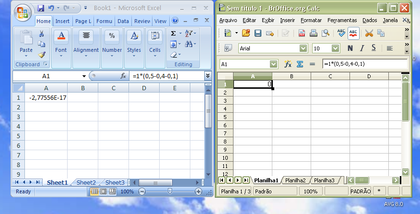
“Responda rápido: quanto é 1*(0,5-0,4-0,1)? Para a maioria de nós, zero, mas não para o Microsoft Excel, que considera o resultado como -2,7755*10^-17.
O que aparentemente pode ser considerado um bug apoia-se em uma norma técnica, a IEEE 754, que regulamenta como os programas de computador devem tratar números com ponto flutuante.
Curiosamente, o software livre de cálculos Octave apresenta o mesmo resultado que o Excel e a calculadora do Gnome mostra como resposta -0, o que pode sugerir um arredondamento ou truncamento. E então, quem está certo e quem está errado?”
Enviado por André Machado (andreferreiramachadoΘgmail·com) – referência (tuxtoriais.wordpress.com).
 @brlinuxblog
@brlinuxblog




Eu acredito que os dois estão corretos, deve se observar a configuração padrão da celula, e vê como cada uma esta configurada, pois, é um numero tão pequeno quanto eu queria, veja -2*10^-17 ou seja um numero com 17 casa decimais.
Humm…
$ bc
bc 1.06.94
Copyright 1991-1994, 1997, 1998, 2000, 2004, 2006 Free Software Foundation, Inc.
This is free software with ABSOLUTELY NO WARRANTY.
For details type `warranty'.
1*(0.5-0.4-0.1)
0
quit
Próximo…
Pra quem já programou em baixo nível sabe que ponto flutuante na informática é dureza.
Mas o que me chamou mais a atenção foi a diferença de interface do Office 2007 pro “concorrente”.
A discussão sobre este fenômeno matemático ocorrido no MS Excel iniciou-se em um tópico do Orkut, na comunidade Linux versus Windows:
http://www.orkut.com.br/Main#CommMsgs.aspx?cmm=18655944&tid=5297825684124574372
Minha opinião pessoal está no referido tópico.
Rodrigo,
Falando como Físico, sua resposta seria aceitável pra muitas coisas da vida prática. Dizer que -2,7755*10^-17 é aproximadamente igual a zero parece ser algo razoável. Mas este número, que é muito pequeno, não é zero. E podem atrapalhar alguns cálculos científicos.
Pra vc ter uma idéia, considere como exemplo o comprimento de onda da luz de um laser de He-Ne (632,8*10^-9 nm). Em alguns cálculos, temos que elevar este número ao quadrado, o que dá 4,0043584*10^-13. Ou seja, se eu tiver que somar a isto o número -2,7755*10^-17, terei afetado minha conta na 4ª casa decimal, o que poderia ser um problema, dependendo do caso.
Este foi apenas um exemplo. Existem áreas que trabalham com fatores ainda menores que isto.
Além do mais, se esta conta do excel está errada, pode se imaginar que existam outros erros, quem sabe até piores (já ouvi falar antes de uma coisa parecida).
Aliás, no BrOffice a conta dá 0,00E+00. Independe da configuração da célula…
Em sistemas dinâmicos caóticos, essa “pequena” diferença muda totalmente o resultado e a precisão dos seus cálculos. Se você quiser estimar a posição de um corpo celeste daqui alguns anos, esta posição pode ser praticamente qualquer lugar no universo visível…
Eu nunca li essa norma técnica e minha experiência com cálculo numérico é limitada, mas eu acredito que não deveria haver arredondamentos ou truncagem devido a precisão de ponto flutuante numa expressão estupidamente simples. Essa conta só exige precisão de um digíto significativo! Se você computar primeiro a expressão dentro dos parênteses, na ordem em que ela é dada, você obtém 0 e 1 vezes 0 é 0. Se você computar primeiro a multiplicação por 1, a conta não muda!
Curiosamente, executem este simples código Javascript no navegador de vocês e vejam o resultado que aparece:
javascript:document.write(1*(0.5-0.4-0.1));Marcos Alexandre, a questão da interface não está sendo discutida. Entretanto, eu prefiro a interface do OpenOffice.org, questão de gosto isso…
Mas o fato é que ambas as planilhas fazem uso da norma ISO 754. Ah, e me parece que o MS Office não implementa totalmente tal norma, embora eu não tenha certeza disso.
Pelo que dá para ver, o MS Office exibe por padrão um formato não muito amigável para o usuário final, a notação científica. Formatando para valor numérico, o valor que aparece é 0, mas este zero é, na verdade, um valor arredondado do número próximo de zer, mas que não é zero.
Já o OpenOffice.org, que por padrão apresenta o número formatado como valor numérico, mais amigável para o usuário final, caso a formatação seja alterada para notação científica, o número exibido é zero, no caso, 0,00E+000.
Tentei na calculadora do Gnome e vi o resultado -0. Ao escolher o formato científico para vizualização obtive o resultado: -1,991364889e-59
$ tcc -run -#include <stdio.h>
int main() {
printf("%e ", 1*(0.5-0.4-0.1));
}
-2.775558e-17
$ js
js> 1*(0.5-0.4-0.1)
-2.7755575615628914e-17
js>
$ ghci
GHCi, version 6.10.1: http://www.haskell.org/ghc/ :? for help
Loading package ghc-prim ... linking ... done.
Loading package integer ... linking ... done.
Loading package base ... linking ... done.
Prelude> 1*(0.5-0.4-0.1)
-2.7755575615628914e-17
Prelude> ^DLeaving GHCi.
$
O Python 2.5 apresenta -2.7755575615628914e-17
A propósito, o Scilab também responde da mesma forma:
-->1*(0.5-0.4-0.1)ans =
- 2.776D-17
Por que notação científica seria “menos amigável para o usuário final”? Notação científica se aprende no Ensino Fundamental. Eu acho mais correto o comportamento do Excel, que não mascara o resultado e mostra o que realmente está contido na célula.
O que pode ser considerado “menos amigável” seja talvez o fato de o Excel considerar o ano 1900 como um ano bissexto, ou o fato de a função DESV.MÉDIO calcular o número de combinações (n k) ao invés de calcular o desvio médio de uma lista de valores…
$ js
Rhino 1.7 release 1 2008 10 20
js> t = 3/10;
0.3
js> u = 1/10;
0.1
js> (3*u - t)/(2*u - t + u);
2
js>
@Jack Ripoff
“Eu acho mais correto o comportamento do Excel,”
Calma vamos pensar matemática simples o valor deve ser 0 mesmo, desde quando 0,5 ou 5/10 menos 0,4 ou 4/10 dá diferente de 1/10?
EX no java 0.5-0.4 dá 0.09999999999999998 mas o valor correto é 0.1
ou seja o Excel está errado, ou vão falar qualquer professor de matemática que 5/10-4/10 não dá 1/10?
posso ser programador usar bits blabla mas matemática básica não foi alterada ainda :)
Depois me passa o contato da escola onde você fez o curso “Como tirar as coisas do contexto”.
</sarcasmo>
Se você reler o meu comentário, vai ver que eu me referia especificamente ao fato de o Excel exibir por padrão o conteúdo da célula em notação científica, em contraste com o Calc que exibe o número arredondado por padrão.
Além disso, para sua informação, 0,0999… é exatamente igual a 0,1. Eu já fui professor de matemática e se você quiser eu forneço a demonstração algébrica ;).
(Note no entanto que o resultado fornecido pelo Java foi truncado e arredondado (???) no 16º significativo, não sendo portanto a mesma coisa…)
Ref.: http://blogs.msdn.com/excel/archive/2007/09/25/calculation-issue-update.aspx
De fato, o OpenOffice usa wrappers em torno das operações matemáticas, para tentar reduzir os erros de arredondamento causados pelos cálculos com ponto flutuante padrão IEEE 754 (que são feitos pela unidade de ponto flutuante do seu processador, e não implementados por um programa ou outro).
Fiz uma pesquisa no Google CodeSearch e encontrei que esses wrappers podem ser encontrados no arquivo include/rtl/math.hxx do código do OpenOffice:
http://www.google.com/codesearch/p?hl=pt-BR#g605e157DJA/OpenOffice.org1.1.2_SDK/include/rtl/math.hxx&q=math%20package:openoffice
Se quiser simular esse comportamento, utilize o seguinte código:
#include <cstdio>inline bool approxEqual(double a, double b)
{
if ( a == b )
return true;
double x = a - b;
return (x < 0.0 ? -x : x)
< ((a < 0.0 ? -a : a) * (1.0 / (16777216.0 * 16777216.0)));
}
inline double approxSub(double a, double b)
{
if ( ((a < 0.0 && b 0.0 && b > 0.0)) && approxEqual( a, b ) )
return 0.0;
return a - b;
}
int main() {
printf("%e ", 1*(approxSub(approxSub(0.5, 0.4), 0.1)));
return 0;
}
Salve num arquivo approx.cpp, compile e rode:
$ g++ approx.cpp -o approx
$ ./approx
0.000000e+00
Pronto. Você reproduziu o comportamento do OpenOffice.
O que acontece é que o Microsoft Office não deve possuir esse tipo de wrapper, exibindo ao usuário exatamente o valor calculado pela FPU, e aconteceria dessa mesma forma se você fizesse um programa para calcular (como eu e outros aqui mostramos em C, JavaScript, Haskell e Python).
O comportamento do OpenOffice somente é reproduzível se você utilizar os mesmos wrappers, como eu fiz no código acima.
Agora a minha opinião – o OpenOffice deveria ter uma opção para desabilitar o uso desses wrappers caso o usuário desejar, pois isso eventualmente pode causar problemas ao importar arquivos do Microsoft Excel, ou ao comparar resultados obtidos em uma planilha com resultados obtidos usando outros programas.
Como é difícil colar códigos aqui no WordPress do BR-Linux, colei o código que simula o comportamento do OpenOffice aqui:
http://brlinux.pastebin.com/f4bcc56b8
Recomendo ao Augusto, se possível, instalar o seguinte plugin:
http://ideathinking.com/wiki/index.php/WordPress:CodeHighlighterPlugin
Segundo fontes, o PHP também apresenta o resultado do Excel.
# python
Python 2.3.4 (#1, Jul 25 2008, 14:24:21)
[GCC 3.4.6 20060404 (Red Hat 3.4.6-10)] on linux2
Type “help”, “copyright”, “credits” or “license” for more information.
>>> 1*(0.5-0.4-0.1)
-2.7755575615628914e-17
>>>
Faltou a resultado do Google!
http://www.google.com.br/search?hl=pt-BR&q=1*(0%2C5-0%2C4-0%2C1)&btnG=Pesquisar&meta=
:)
Só para complementar, o bc retorna zero pois ele não utiliza a FPU do seu computador para fazer as contas.
O bc utiliza aritmética de precisão arbitrária que é implementada pelo seu código em:
http://www.google.com/codesearch/p?hl=en#CN-HQ4zhgJs/bc-1.06/lib/number.c&q=package:bc-1.06.tar.gz
Em especial, dê uma olhada no _bc_do_sub.
Jack Ripoff, gostaria de ver sua demonstração que 0,0999 é igual a 0,1.
Agradeço aos usuário que mostraram que não é apenas o excel quem faz as contas “erradas”. Nunca tinha prestado atenção nisso. A coisa é mais feia do que eu pensava…
Alan, não foi isso que ele afirmou. Ele apresentou uma dízima periódica (0,0999…) e não o 0,0999.
0,0999 não é igual a 0,1
0,0999… (dizíma periódica, infinitos noves) é igual a 0,1. Demonstração:
Seja x = 0,0999…
Vamos multiplicar nossa igualdade por 10.
10x = 0,999…
Vamos subtrair x dos dois lados da nossa equação.
10x – x = 0,999… – x
9x = 0,999… – 0,0999…
Mas 0,999… menos 0,0999… é igual a 0,9. Portanto
9x = 0,9
x = 0,9 / 9 => x = 0,1
Q.E.D.
Na verdade 0,0999… é simplesmente outra forma de representar o mesmo número que 0,1. Isto fica evidente se você pensar na arquimedianidade e na completude do conjunto dos números reais. Por essas propriedades não pode existir um número real imediatamente inferior a outro, pois a diferença entre os dois seria um infinitesimal e não existem infinitesimais no conjunto dos reais. Se a diferença fosse diferente de zero, é sempre possível imaginar um número entre os outros dois e cuja diferença entre eles seja menor mas ainda diferente de zero.
O corolário disto é que todos os números racionais cuja representação decimal não é uma dízima periódica possuem uma segunda representação decimal que é uma dízima periódica (com infinitos noves), mas a demonstração disto fica para outro dia.
Augusto e Jack, sendo dízima periódica a explicação está correta, porém, lastimavelmente, virou lugar-comum substituir a vírgula por reticências. Logo, não sabia se o Jack havia escrito a dízima ou feito a famigerada substituição.
Abraços,
Estou vendo que esse assunto deu bastante controvérsia.
É algo simples, que está definido de forma clara, mas que poucas pessoas sequer fazem idéia do que acontece.
Numeros REAIS (ponto flutuante) em computadores sempre foi um campo tortuoso. É preciso conhecer bem MATEMÁTICA e ainda melhor COMPUTAÇÃO para entender porque essas coisas acontecem.
Temos que lembrar que os computadores realizam contas na base 2 e não na base 10. Se a conta apresentada for feita usando a base 2 haverá a geração de dizimas e necessidade de arredondamentos/truncamentos em alguma parte.
E sendo sarcástico, alguém que precise fazer cáculos avançados onde isso faça realmente uma grande diferença deve saber matemática o suficiente para entender porque isso acontece e deveria conhecer computação o suficiente para escolher uma ferramenta de cálculo mais adequada.
http://www.google.com.br/search?q=1*(0.5-0.4-0.1)
aqui deu zero :P
Agora a minha opinião – o OpenOffice deveria ter uma opção para desabilitar o uso desses wrappers caso o usuário desejar, pois isso eventualmente pode causar problemas ao importar arquivos do Microsoft Excel, ou ao comparar resultados obtidos em uma planilha com resultados obtidos usando outros programas.
Seria bom requisitar essa funcionalidade aos desenvolvedores do OpenOffice.org!
“E sendo sarcástico, alguém que precise fazer cáculos avançados onde isso faça realmente uma grande diferença deve saber matemática o suficiente para entender porque isso acontece e deveria conhecer computação o suficiente para escolher uma ferramenta de cálculo mais adequada.”
Exato. Pra isso existem softwares próprios pra cálculo científico. Ninguém vai traçar a rota pra um planeta no Excel. Trabalhar em outra base que não a binaria no computador dá diferença de performance. Mesmo wrappers você está reduzindo a performance. Como a margem de erro é mínima pros usuários comuns, a maioria dos softwares pro público geral não se importam.
Outra demostração da igualdade é que um número é igual a outro quando a diferença entre eles for zero.
0,1 – 0,09999… = 0,000…
hehehehe
Outro exemplo interessante.
1/3 = 0,3333….
1/3 + 1/3 + 1/3 = 0,99999…..
Mas se você somar os “terços” dá 3/3 que é igual a 1
Infinitesimais na matemática é muito doido!
Mas nós constatamos que até o Octave e o Scilab, que são programas “próprios” para computação científica, apresentam esse comportamento.
Outra demonstração interessante da igualdade usa séries infinitas. O número 0,999… pode ser escrito assim:
0,999… = 9/10 + 9/100 + 9/1000 + …
Mas pelo teorema da convergência das progressões geométricas com razão de módulo menor que 1, essa série converge e a soma infinita é dada pela fórmula:
(9/10)/(1 – 1/10) = 1
Q.E.D.
No google
1 * (0.5 – 0.4 – 0.1) = 0
Na calculadora do Gnome no normal aparece 0 .No cietifico com o padrão cientifico selecionado -1,416423594e-219
Interessante este cálculo.
Alguém poderia explicar como 1*(0,5-0,4-0,1) resulta -2,7755*10^-17?
Poder ser um link até em inglês mesmo. Grato.
Sou fã de matemática.
Como o colega disse acima seria muito bom e o OO.o tivesse opção para desativar tais aproximações. Apesar de seguir a norma isso pode ser considerado um bug pois mesmo alterando o modo de exibição ele mostra um valor impreciso.
Tambem acho a matematica que eu saiba continua a mesma e o valor logico eh:
0.5 – 0.4 = 0,1
1*(0,1 – 0,1) = 0 Em qualquer conta
http://support.microsoft.com/kb/78113